See also: History of Earth
The Blue Marble, Earth as seen from Apollo 17
The age of the Earthis estimated to be 4.54 ± 0.05 billion years (4.54 × 109years ± 1%).[1][2][3][4] This age may represent the age of the Earth's accretion, or core formation, or of the material from which the Earth formed.This dating is based on evidence from radiometric age-dating of meteorite material and is consistent with the radiometric ages of the oldest-known terrestrial and lunar samples.
Following the development of radiometric age-dating in the early 20th century, measurements of lead in uranium-rich minerals showed that some were in excess of a billion years old. The oldest such minerals analyzed to date—small crystals of zircon from the Jack Hills of Western Australia—are at least 4.404 billion years old. Calcium–aluminium-rich inclusions—the oldest known solid constituents within meteorites that are formed within the Solar System—are 4.567 billion years old,giving a lower limit for the age of the Solar System.
It is hypothesised that the accretion of Earth began soon after the formation of the calcium-aluminium-rich inclusions and the meteorites. Because the time this accretion process took is not yet known, and predictions from different accretion models range from a few million up to about 100 million years, the difference between the age of Earth and of the oldest rocks is difficult to determine. It is also difficult to determine the exact age of the oldest rocks on Earth, exposed at the surface, as they are aggregates of minerals of possibly different ages.
Solar System
From Wikipedia, the free encyclopedia
Solar System
(distances not to scale) | |
Age | 4.568 billion years |
Location | Local Interstellar Cloud, Local Bubble, Orion–Cygnus Arm, Milky Way |
System mass | 1.0014 Solar masses |
Nearest star | Proxima Centauri(4.25 ly) Alpha Centauri(4.37 ly) |
Nearest known planetary system | Proxima Centauri system (4.25 ly) |
Planetary system | |
Semi-major axis of outer known planet (Neptune) | 30.10 AU (4.5 bill. km; 2.8 bill. mi) |
Distance to Kuiper cliff | 50 AU |
Populations | |
Stars | 1 (Sun) |
Known planets | |
Known dwarf planets | 3 universally accepted 2 more expected to be |
Known natural satellites | • 575 (185 planetary390 minor planetary)[1][2] |
Known minor planets | 796,354[a][3] |
Known comets | 4,143[a][3] |
Identified rounded satellites | 19 (5–6 likely in hydrostatic equilibrium) |
Orbit about Galactic Center | |
Invariable-to-galactic planeinclination | 60.19° (ecliptic) |
Distance to Galactic Center | 27,000 ± 1,000 ly |
Orbital speed | 220 km/s; 136 mps |
Orbital period | 225–250 myr |
Star-related properties | |
≈5 AU[4] | |
Distance to heliopause | ≈120 AU |
Hill sphere radius | ≈1–3 ly |
Solar System
Objects |
Lists |
Planets |
The Solar System[b]is the gravitationally bound system of the Sun and the objects that orbit it, either directly or indirectly. Of the objects that orbit the Sun directly, the largest are the eight planets, with the remainder being smaller objects, the dwarf planets and small Solar System bodies. Of the objects that orbit the Sun indirectly—the moons—two are larger than the smallest planet, Mercury.[e]
The Solar System formed 4.6 billion years ago from the gravitational collapse of a giant interstellar molecular cloud. The vast majority of the system's mass is in the Sun, with the majority of the remaining mass contained in Jupiter. The four smaller inner planets, Mercury, Venus, Earth and Mars, are terrestrial planets, being primarily composed of rock and metal. The four outer planets are giant planets, being substantially more massive than the terrestrials. The two largest, Jupiter and Saturn, are gas giants, being composed mainly of hydrogen and helium; the two outermost planets, Uranus and Neptune, are ice giants, being composed mostly of substances with relatively high melting points compared with hydrogen and helium, called volatiles, such as water, ammonia and methane. All eight planets have almost circular orbits that lie within a nearly flat disc called the ecliptic.
The Solar System also contains smaller objects.[f]The asteroid belt, which lies between the orbits of Mars and Jupiter, mostly contains objects composed, like the terrestrial planets, of rock and metal. Beyond Neptune's orbit lie the Kuiper belt and scattered disc, which are populations of trans-Neptunian objects composed mostly of ices, and beyond them a newly discovered population of sednoids. Within these populations, some objects are large enough to have rounded under their own gravity, though there is considerable debate as to how many there will prove to be.[9][10]Such objects are categorized as dwarf planets. Identified or accepted dwarf planets include the asteroid Ceres and the trans-Neptunian objects Pluto and Eris. In addition to these two regions, various other small-body populations, including comets, centaurs and interplanetary dust clouds, freely travel between regions. Six of the planets, the six largest possible dwarf planets, and many of the smaller bodies are orbited by natural satellites, ]usually termed "moons" after the Moon. Each of the outer planets is encircled by planetary rings of dust and other small objects.
The solar wind, a stream of charged particles flowing outwards from the Sun, creates a bubble-like region in the interstellar medium known as the heliosphere. The heliopauseis the point at which pressure from the solar wind is equal to the opposing pressure of the interstellar medium; it extends out to the edge of the scattered disc. The Oort cloud, which is thought to be the source for long-period comets, may also exist at a distance roughly a thousand times further than the heliosphere. The Solar System is located in the Orion Arm, 26,000 light-years from the center of the Milky Way Galaxy.
Asteroid belt
From Wikipedia, the free encyclopedia
The asteroids of the inner Solar System and Jupiter: The belt is located between the orbits of Jupiter and Mars.
Asteroid belt Hilda asteroids(Hildas) Near-Earth objects(selection) |
The relative masses of the top twelve asteroids known compared to the remaining mass of all the other asteroids in the belt.[1
By far the largest object within the belt is Ceres. The total mass of the asteroid belt is significantly less than Pluto's, and approximately twice that of Pluto's moon Charon.
The asteroid beltis a torus-shaped region in the Solar System, located roughly between the orbits of the planets Jupiterand Mars, that is occupied by a great many solid, irregularly shaped bodies, of many sizes but much smaller than planets, called asteroids or minor planets. This asteroid belt is also called the main asteroid beltor main beltto distinguish it from other asteroid populations in the Solar System such as near-Earth asteroids and trojan asteroids.[2]
About half the mass of the belt is contained in the four largest asteroids: Ceres, Vesta, Pallas, and Hygiea.[2]The total mass of the asteroid belt is approximately 4% that of the Moon, or 22% that of Pluto, and roughly twice that of Pluto's moon Charon(whose diameter is 1200 km)
THE TWINS - PLUTO AND CERES
PLUTO IS ON THE LEFT AND CERES ON THE RIGHTCeres, the only object in the asteroid belt large enough to be a dwarf planet, is about 950 km in diameter, whereas Vesta, Pallas, and Hygiea have mean diameters of less than 600 km.[3][4][5][6]The remaining bodies range down to the size of a dust particle. The asteroid material is so thinly distributed that numerous unmanned spacecraft have traversed it without incident.[7]Nonetheless, collisions between large asteroids do occur, and these can produce an asteroid familywhose members have similar orbital characteristics and compositions. Individual asteroids within the asteroid belt are categorized by their spectra, with most falling into three basic groups: carbonaceous(C-type), silicate(S-type), and metal-rich (M-type).
The asteroid belt formed from the primordial solar nebulaas a group of planetesimals.[8]Planetesimals are the smaller precursors of the protoplanets. Between Mars and Jupiter, however, gravitational perturbations from Jupiter imbued the protoplanets with too much orbital energy for them to accrete into a planet.[8][9]Collisions became too violent, and instead of fusing together, the planetesimals and most of the protoplanets shattered. As a result, 99.9% of the asteroid belt's original mass was lost in the first 100 million years of the Solar System's history.[10]Some fragments eventually found their way into the inner Solar System, leading to meteorite impacts with the inner planets. Asteroid orbits continue to be appreciably perturbed whenever their period of revolution about the Sun forms an orbital resonance with Jupiter. At these orbital distances, a Kirkwood gap occurs as they are swept into other orbits.[11]
Classes of small Solar System bodiesin other regions are the near-Earth objects, the centaurs, the Kuiper beltobjects, the scattered discobjects, the sednoids, and the Oort cloudobjects.
On 22 January 2014, ESA scientists reported the detection, for the first definitive time, of water vaporon Ceres, the largest object in the asteroid belt.[12]The detection was made by using the far-infrared abilities
Kuiper belt
From Wikipedia, the free encyclopedia
Known objects in the Kuiper belt beyond the orbit of Neptune. (Scale in AU; epochas of January 2015.)
Resonant Kuiper belt Classical Kuiper belt |
Distances but not sizes are to scale
Source: Minor Planet Center, www.cfeps.netand others
Types of distant minor planets
• Trans-Neptunian objects (TNOs) Kuiper belt objects (KBOs) Classical KBOs (cubewanos) Plutinos (2:3 resonance) Scattered disc objects (SDOs) Extreme trans-Neptunian object Oort cloud objects (ICO/OCOs) |
The Kuiper belt(/ˈkaɪpər, ˈkʊɪ-/),[ occasionally called the Edgeworth–Kuiper belt, is a circumstellar disc in the outer Solar System, extending from the orbit of Neptune (at 30 AU) to approximately 50 AU from the Sun.[2]It is similar to the asteroid belt, but is far larger—20 times as wide and 20 to 200 times as massive.[3][4]Like the asteroid belt, it consists mainly of small bodies or remnants from when the Solar System formed. While many asteroids are composed primarily of rock and metal, most Kuiper belt objects are composed largely of frozen volatiles (termed "ices"), such as methane, ammonia and water. The Kuiper belt is home to three officially recognized dwarf planets: Pluto, Haumea and Makemake. Some of the Solar System's moons, such as Neptune's Triton and Saturn's Phoebe, may have originated in the region.[5][6]
The Kuiper belt was named after Dutch-American astronomer Gerard Kuiper, though he did not predict its existence. In 1992, Albion was discovered, the first Kuiper belt object (KBO) since Pluto and Charon.[7]Since its discovery, the number of known KBOs has increased to thousands, and more than 100,000 KBOs over 100 km (62 mi) in diameter are thought to exist.[8]The Kuiper belt was initially thought to be the main repository for periodic comets, those with orbits lasting less than 200 years. Studies since the mid-1990s have shown that the belt is dynamically stable and that comets' true place of origin is the scattered disc, a dynamically active zone created by the outward motion of Neptune 4.5 billion years ago;[9]scattered disc objects such as Eris have extremely eccentric orbits that take them as far as 100 AU from the Sun.[nb 1]
The Kuiper belt is distinct from the theoretical Oort cloud, which is a thousand times more distant and is mostly spherical. The objects within the Kuiper belt, together with the members of the scattered disc and any potential Hills cloud or Oort cloud objects, are collectively referred to as trans-Neptunian objects(TNOs).[12]Pluto is the largest and most massive member of the Kuiper belt, and the largest and the second-most-massive known TNO, surpassed only by Eris in the scattered disc.[nb 1]Originally considered a planet, Pluto's status as part of the Kuiper belt caused it to be reclassified as a dwarf planet in 2006. It is compositionally similar to many other objects of the Kuiper belt and its orbital period is characteristic of a class of KBOs, known as "plutinos", that share the same 2:3 resonance with Neptune.
The Kuiper belt and Neptune may be treated as a marker of the extent of the Solar System, alternatives being the heliopause and the distance at which the Sun's gravitational influence is matched by that of other stars (estimated to be between 50000 AU and about 2 light-years).[13]
OUR MILKY WAY GALAXY
WHAT IS A GALAXY?
What Is a Galaxy?
We live on a planet called Earth that is part of our solar system.
But where is our solar system? It’s a small part of the Milky Way Galaxy.
A galaxy is a huge collection of gas, dust, and billions of stars and their solar systems. A galaxy is held together by gravity. Our galaxy, the Milky Way, also has a supermassive black hole in the middle.
SUPER BLACK HOLE IN OUR GALAXY
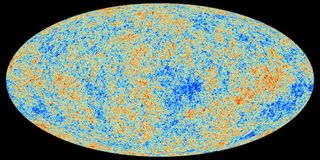
The Big Bang Theory is the leading explanation about how the universe began. At its simplest, it says the universe as we know it started with a small singularity, then inflated over the next 13.8 billion years to the cosmos that we know today.
Because current instruments don't allow astronomers to peer back at the universe's birth, much of what we understand about the Big Bang Theory comes from mathematical formulas and models. Astronomers can, however, see the "echo" of the expansion through a phenomenon known as the cosmic microwave background
Age of the universe
| Part of a series on |
| Physical cosmology |
|---|
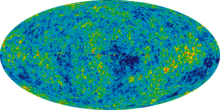 |
In physical cosmology, the age of the universe is the time elapsed since the Big Bang. The current measurement of the age of the universe is around 13.8 billion years (as of 2015[1]) – 13.787±0.020billion years within the Lambda-CDM concordance model (as of 2018.[2])The uncertainty has been narrowed down to 20 million years, based on a number of studies which all gave extremely similar figures for the age. These include studies of the microwave background radiation by the Planck spacecraft, the Wilkinson Microwave Anisotropy Probe and other space probes. Measurements of the cosmic background radiation give the cooling time of the universe since the Big Bang,[3] and measurements of the expansion rate of the universe can be used to calculate its approximate age by extrapolating backwards in time.
The Lambda-CDM concordance model describes the evolution of the universe from a very uniform, hot, dense primordial state to its present state over a span of about 13.8 billion years[4] of cosmological time. This model is well understood theoretically and strongly supported by recent high-precision astronomical observations such as WMAP. In contrast, theories of the origin of the primordial state remain very speculative. If one extrapolates the Lambda-CDM model backward from the earliest well-understood state, it quickly (within a small fraction of a second) reaches a singularity. This is known as the "initial singularity" or the "Big Bang singularity". This singularity is not understood as having a physical significance in the usual sense, but it is convenient to quote times measured "since the Big Bang" even though they do not correspond to a physically measurable time. For example, "10−6 seconds after the Big Bang" is a well-defined era in the universe's evolution. If one referred to the same era as "13.8 billion years minus 10−6 seconds ago", the precision of the meaning would be lost because the minuscule latter time interval is eclipsed by uncertainty in the former.
Though the universe might in theory have a longer history, the International Astronomical Union[5] presently use "age of the universe" to mean the duration of the Lambda-CDM expansion, or equivalently the elapsed time since the Big Bang in the current observable universe.
Since the universe must be at least as old as the oldest things in it, there are a number of observations which put a lower limit on the age of the universe; these include the temperature of the coolest white dwarfs, which gradually cool as they age, and the dimmest turnoff point of main sequence stars in clusters (lower-mass stars spend a greater amount of time on the main sequence, so the lowest-mass stars that have evolved away from the main sequence set a minimum age).
The problem of determining the age of the universe is closely tied to the problem of determining the values of the cosmological parameters. Today this is largely carried out in the context of the ΛCDM model, where the universe is assumed to contain normal (baryonic) matter, cold dark matter, radiation (including both photons and neutrinos), and a cosmological constant. The fractional contribution of each to the current energy density of the universe is given by the density parameters Ωm, Ωr, and ΩΛ. The full ΛCDM model is described by a number of other parameters, but for the purpose of computing its age these three, along with the Hubble parameter , are the most important.
If one has accurate measurements of these parameters, then the age of the universe can be determined by using the Friedmann equation. This equation relates the rate of change in the scale factor a(t) to the matter content of the universe. Turning this relation around, we can calculate the change in time per change in scale factor and thus calculate the total age of the universe by integrating this formula. The age t0 is then given by an expression of the form
where is the Hubble parameter and the function F depends only on the fractional contribution to the universe's energy content that comes from various components. The first observation that one can make from this formula is that it is the Hubble parameter that controls that age of the universe, with a correction arising from the matter and energy content. So a rough estimate of the age of the universe comes from the Hubble time, the inverse of the Hubble parameter. With a value for around 69 km/s/Mpc, the Hubble time evaluates to = 14.5 billion years.[6]
The reason I have given out this information is for the opening of the minds of man to how really old are Universe, Galaxies, Solar System and our Sun and Planets are, and that for at least
III Time, from the first appearance of "humanity(on planetary chain) 1,664,500,987 Years
years there was life forms on this Earth know as Root Races. I will be giving you the explanation for a Manvantara with its periods of time separated by Pralayas known as Yugas. Each Yuga representatives an eon of time in which people and/or Root Races existed, lived and after about 14,000 years ascended back to God - in fact, the first three Root Races were prime examples of man coming into the planet, expressing some God-Quality and leaving the planet better off than when they arrived; because our main purpose for being on Earth is to bring a particular God-Quality with us that we can express and give to the planet as a gift that can help future generations. We need to remember that the first three Root Races were of a more androgynous make-up and were more ethereal than having bones and flesh bodies - again, this also had to do with the planet itself, as it was still cooling down and our bodies would never have survived the temperatures at that time.
The Third Root Race existed on LeMuria:
End of lesson

















No comments:
Post a Comment